四旋翼无人机建模与仿真(Mathematica/Matlab)

2018-09-15

本博客所有文章采用的授权方式为 自由转载-非商用-非衍生-保持署名 ，转载请务必注明出处，谢谢。

声明：
本博客欢迎转发，但请保留原作者信息!
博客地址：焦海林的博客;
内容系本人学习、研究和总结，如有雷同，实属荣幸！

四旋翼无人机建模与仿真(Mathematica/Matlab)

1. 四旋翼的数学模型

四旋翼无人机的受力模型如下图所示，

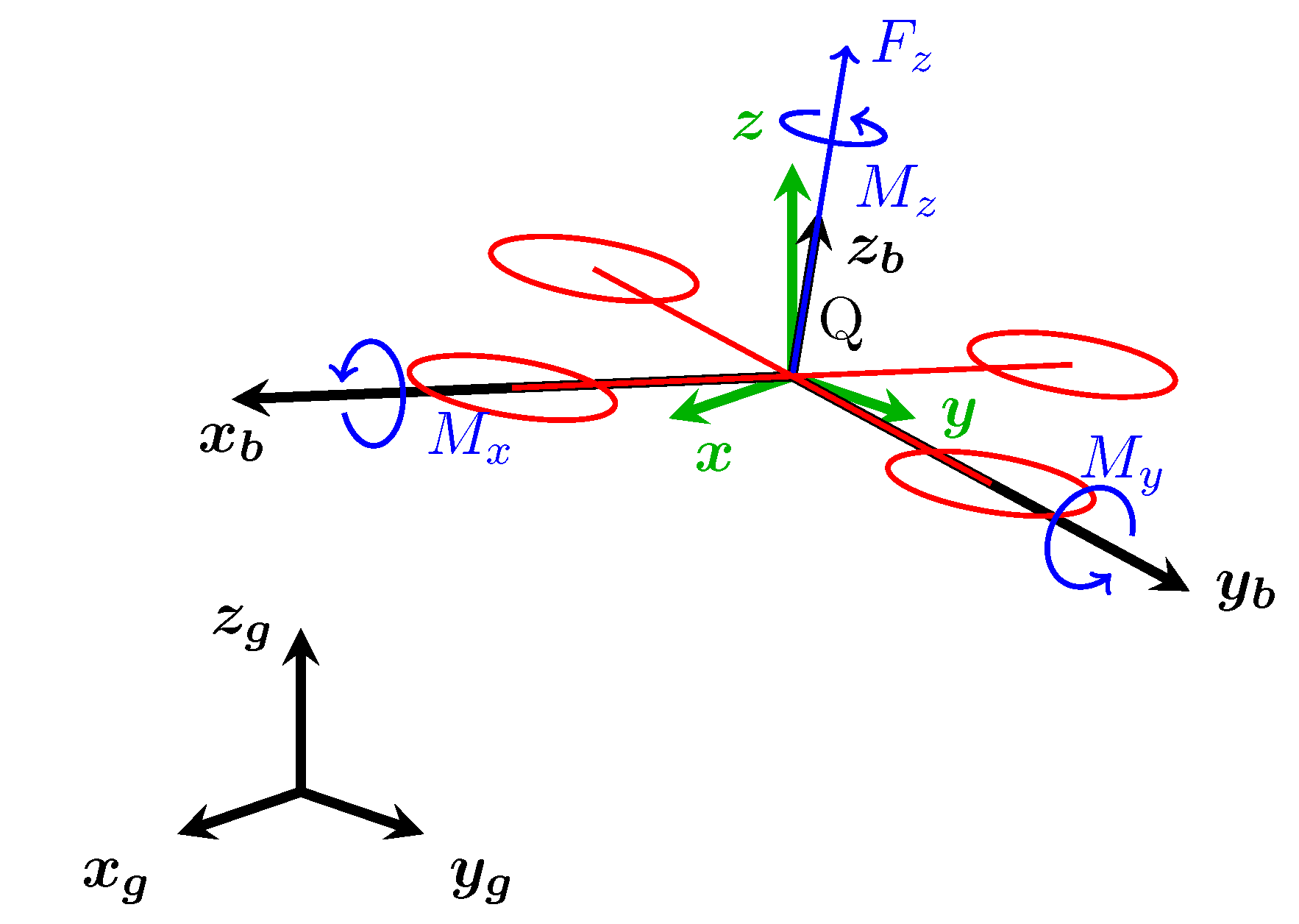
Fig. 1: 四旋翼无人机示意图

1.1 坐标系

地面坐标系(惯性坐标系)—— $\{\mathscr{G}:x_{g}y_{g}z_{g}\}$ 该坐标系的三个正交单位基向量记作 $\{\bf{E}_x,\bf{E}_y,\bf{E}_z\}$ 。
机体坐标系—— $\{\mathscr{B}:x_{b}y_{b}z_{b}\}$ 该坐标系的三个正交单位基向量记作${\bf{e}_x,\bf{e}_y,\bf{e}_z}$。
过渡坐标系—— $\{\mathscr{S}:xyz\}$ 代表以四旋翼无人机的质心Q为原点，方向与${\mathscr{G}}$相同的过渡坐标系。

1.2 四旋翼无人机的位置、姿态角

四旋翼无人机的位置记作 $\bf{\xi}_Q=[x_Q,y_Q,z_Q]^T\in \mathbb{R}^3$ ，
四旋翼无人机的姿态角 按照”横滚-俯仰-偏航’‘的顺序定义为 $\bf{\eta}=[\phi,\theta,\psi]^T\in \mathbb{R}^3$ 。

1.3 四旋翼无人机的控制输入

螺旋桨转速

四旋翼无人机是通过四个电机带动螺旋桨进行控制的，每个螺旋桨在机体坐标系内形成一个升力 $f_i$ 和一个力矩 ${\tau} _{M_i}$ ，其方向均沿着 $\bf{z}_b$ 方向，大小与螺旋桨转速的二次方成正比，
$\begin{equation} \begin{aligned} {f_i} &= {k_f} n_i^2\\ {\tau}_{M_i} &= k_{\tau} n_i^2\\ \end{aligned} \end{equation}$
其中，下标 $i=1,...,4$ 表示四个螺旋桨， $n_i$ 表示螺旋桨的转速， $k_f$ 和 $k_{\tau}$ 是与螺旋桨的尺寸和类型相关的物理参数。
等效力和等效力矩

通过将四个螺旋桨产生的升力 $f_i$ 和力矩 ${\tau}_{M_i}$ 进行线性组合，可以得到作用在机体坐标系内的力和力矩 $\bf{U}=[F_z,M_x,M_y,M_z]^T$ ，即

$\begin{equation} \left[ {\begin{array}{*{20}{c}} {F_z}\\ {M_x}\\ {M_y}\\ {M_z} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^4 {f_i}}\\ {(f_2-f_4)l_a}\\ {(f_1-f_3)l_a}\\ {\sum\limits_{i = 1}^4{\tau_{Mi}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {k_f}&{k_f}&{k_f}&{k_f}\\ 0&{k_fl_a}&0&{ - k_fl_a}\\ { - k_fl_a}&0&{k_fl_a}&0\\ {k_\tau}&{ - {k_\tau}}&{k_\tau}&-{k_\tau} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {n_1^2}\\ {n_2^2}\\ {n_3^2}\\ {n_4^2} \end{array}} \right] \end{equation}$

其中， $l_a$ 为从螺旋桨中心到四旋翼无人机几何中心的距离。

因此为了方便起见，将直接以等效力和等效力矩作为四旋翼无人机的控制输入变量。

1.4 Euler-Lagrange建模

广义坐标

为了用Euler-Lagrange方法建立该系统的动力学模型，首先需要选择该系统的广义坐标。该系统有6个自由度，选择广义坐标 $\bf{q}_z=\left[{\bf{\xi}^{\mathscr{G}}_Q}^T,{\bf{\eta}}^T\right]^T$ 。
广义力

与广义坐标 $\bf{q}_z$ 对应的广义力 $\mathbf{F}_{\bf{q}_z}$ 为，

$\begin{equation} \bf{F}_{\bf{q}_z} = \frac{\partial \left( {\bf{F}^{\mathscr{G}}_Q \cdot {\mathbf{\xi}^{\mathscr{G}} _{Q}} + {\bf{M}^{\eta}_{Q}} \cdot {\bf{\eta}}} \right)}{\partial {\bf q_z}} \end{equation}$

注：

动能、势能和Lagrangian

因此，作为6自由度刚体，四旋翼无人机的动能 $\mathscr{T}$ 、势能 $\mathscr{U}$ 和Lagrangian可分别写为

$\begin{equation} \begin{aligned} \mathscr{T} &= \frac{1}{2}{m_{Q}}{\dot{\bf{\xi}}^{\mathscr{G}}_{Q}} \cdot {\dot{\bf{\xi}}^{\mathscr{G}} _{Q}} + \frac{1}{2}{\bf{\Omega} ^T}{\bf{I}_{Q}}\bf{\Omega}\\ \mathscr{U} &= {m_{Q}}\bf{g} \cdot {\bf{\xi}^{\mathscr{G}}_{Q}}\\ \mathscr{L} &= \mathscr{T} - \mathscr{U} \end{aligned} \end{equation}$

Euler-Lagrange方程

$\begin{equation} \frac{d}{\text{dt}}(\frac{\partial \mathscr{L}}{\partial \dot{\bf{q}}_z})-\frac{\partial \mathscr{L}}{\partial \bf{q}_z}=\bf{F}_{\bf{q}_z} \label{a} \end{equation}$

式\eqref{a}

四旋翼无人机建模与仿真(Mathematica/Matlab)

四旋翼无人机建模与仿真(Mathematica/Matlab)

1. 四旋翼的数学模型

1.1 坐标系

1.2 四旋翼无人机的位置、姿态角

1.3 四旋翼无人机的控制输入

1.4 Euler-Lagrange建模

文章赞赏

文章评论