拉格朗日

2019-07-12

本博客所有文章采用的授权方式为 自由转载-非商用-非衍生-保持署名 ，转载请务必注明出处，谢谢。

声明：
本博客欢迎转发，但请保留原作者信息!
博客地址：焦海林的博客;
内容系本人学习、研究和总结，如有雷同，实属荣幸！

导言

在这个项目中，我通过拉格朗日运动方程推导出和时间相关的四旋翼飞行器的动力学，同时通过欧拉角描述四旋翼飞行器的姿态。我首先展示了欧拉角，它们的导数，和四旋翼速度之间的关系。利用这些关系，我找到了平移和势能差的表达式。利用这个表达式，通过拉格朗日方法导出了刚体各状态变量的运动方程。

欧拉旋转方程

$\begin{multline} T = \begin{bmatrix} c_\psi & s_\psi & 0 \\ -s_\psi & c_\psi & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & c_\theta & s_\theta \\ 0 & -s_\theta & c_\theta \end{bmatrix} \begin{bmatrix} c_\phi & s_\phi & 0 \\ -s_\phi & c_\phi & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} c_\psi c_\phi - s_\psi c_\theta s_\phi & c_\psi s_\phi + s_\psi c_\theta c_\phi & s_\psi s_\theta \\ -s_\psi c_\phi - c_\psi c_\theta s_\phi & -s_\psi s_\phi + c_\psi c_\theta c_\phi & c_\psi s_\theta \\ s_\theta s_\phi & -s_\theta c_\phi & c_\theta \end{bmatrix} \tag{1} \end{multline}$

欧拉角参数与角速度矢量之间的关系如下

$\begin{equation} \omega = \begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix} = \begin{bmatrix} s_\psi s_\theta \dot \phi + c_\psi \dot \theta \\ c_\psi s_\theta \dot \phi - s_\psi \dot \theta \\ c_\theta \dot \phi + \dot \psi \end{bmatrix} \tag{2} \end{equation}$

拉格朗日运动方程

拉格朗日运动方程是由下列方程导出的：

$\begin{equation} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot q_i}\right) - \frac{\partial L}{\partial q_i} = \Phi_{q_i} \tag{3} \end{equation}$

总系统能量

在上面的方程中，$L$表示动力学之间的差异($T$)和潜力($U$)系统内的能量。因此，$L$可表示为：

$\begin{equation} L = T - U \end{equation}$

此外，$T$，作为平移动能和转动动能的结合，可以表示为：

$\begin{equation} T = T_{translational} + T_{rotational} \end{equation}$

让我们来定义$\overline{x}=x E_x + y E_y + z E_z$作为四翼飞机的质量中心，如下所示。

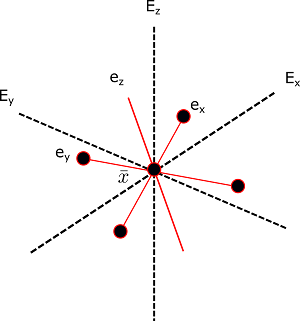
Fig. 1: 四旋翼飞行姿态

quad-attitude因为 $v = \dot{\overline x}= \begin{bmatrix} \dot x \\ \dot y \\ \dot z \\ \end{bmatrix}$ ，我们有

$\begin{equation} T_{translational} = \frac{1}{2}mv \cdot v = \frac{1}{2} m \left(\dot x^2 + \dot y^2 + \dot z^2\right) \end{equation}$

此外，因为 $J=\begin{bmatrix} J_{xx} & 0 & 0\\ 0 & J_{yy} & 0\\ 0 & 0 & J_{zz} \end{bmatrix}$ 由于四边形的对称性， $\omega = \begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix}$ ，我们有

$\begin{equation} T_{rotational} = \frac{1}{2}J\omega \cdot \omega = \frac{1}{2}\left(J_{xx}\omega^2_x + J_{yy}\omega^2_y + J_{zz}\omega^2_z\right) \end{equation}$

因此，总动能可以表示为

$\begin{equation} T = \frac{1}{2} m \left(\dot x^2 + \dot y^2 + \dot z^2\right) + \frac{1}{2} \left(J_{xx}\omega^2_x + J_{yy}\omega^2_y + J_{zz}\omega^2_z\right) \end{equation}$

由于势能，$U$，看作是$mgz$,所以表达式$L$可表示为：

$\begin{equation} L = \frac{1}{2} m (\dot x^2 + \dot y^2 + \dot z^2) + \frac{1}{2} (J_{xx}\omega^2_x + J_{yy}\omega^2_y + J_{zz}\omega^2_z) - mgz \tag{4} \end{equation}$

将方程$(2)$带入方程$(4)$中，我们得到最后的表达式$L$：

$\begin{multline} L = \frac{1}{2} m (\dot x^2 + \dot y^2 + \dot z^2) + \frac{1}{2}J_{xx}s_\psi^2 s_\theta^2 \dot\phi^2 + J_{xx}s_\psi s_\theta c_\psi \dot \phi \dot \theta + \frac{1}{2}J_{xx}c_\psi^2 \dot \theta^2 + \frac{1}{2}J_{yy}c_\psi^2s_\theta^2 \dot\phi^2 - J_{yy} c_\psi s_\theta s_\psi \dot \phi \dot \theta + \frac{1}{2} J_{yy}s_\psi^2 \dot \theta^2 + \frac{1}{2}J_{zz}c_\theta^2 \dot \phi^2 + J_{zz} c_\theta \dot \phi \dot \psi + \frac{1}{2}J_{zz} \dot \psi^2 - mgz \tag{5} \end{multline}$

拉格朗日

导言

文章赞赏

文章评论